- Manufacturer: Ligne Roset City
- Designer: Gregory Lacoua
- Material: plywood, cotton
- Dimensions: 44 × 75 × 75
- www.ligne-roset-city.co.uk

Index
- Ottoman / Table Gregory is an ottoman/table which transforms into a rug (and vice versa) in one simple operation. It will appeal to children of all ages; to ladies, a
- Origami Origami (折り紙, from oru meaning 'folding', and kami meaning 'paper') is the traditional Japanese art of paper folding. The goal of this art is to creat
- Transformers Transformers face an array of issues that demand operating efficiency. Some transformers have two or three modes of transformation, for example: first
Gregory is an ottoman/table which transforms into a rug (and vice versa) in one simple operation. It will appeal to children of all ages; to ladies, as an ideal complement to a dressing table; to those to whom space is at a premium (a compact rug doubling as an additional seat); to those of a poetic nature, who are fascinated by a new, simple and ingenious idea; and finally to the more practical or economic amongst us, who love to get two objects for the price of one.
VIA
VIA (Valorization of Innovation in Furnishing) is a non-profit association that was set up in 1979 by the CODIFA (French Furniture Industries Development Committee), with the support of the Ministry for Industry. The vocation of VIA is to valorize and promote contemporary creation in furnishing (furniture, lighting, tableware, decorative items, rugs, interior textiles …), both in France and abroad. [...]
Our programme of action covers the entire profession: industrial groups, small and medium-sized firms, artisans, producers, distributors, creative people, and extends to the general public (exhibitions, talks) and neighbouring sectors of activity: contemporary life styles, art, fashion...
Gregory: Project Assistance VIA, 2006

Origami (折り紙, from oru meaning 'folding', and kami meaning 'paper') is the traditional Japanese art of paper folding. The goal of this art is to create a representation of an object using geometric folds and crease patterns preferably without gluing or cutting the paper, and using only one piece of paper.

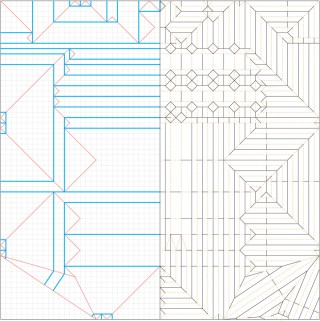
Crease Pattern
A Crease Pattern is an origami diagram type that consists of all or most of the creases in the final model, rendered into one image. This comes in handy for diagramming complex and super-complex models, where the model is often not simple enough to diagram efficiently.
The use of crease patterns originated with designers such as Neal Elias, who used them to record how their models were made. This allowed the more prolific designers to keep track of all their models, and soon crease patterns began to be used as communication of ideas between designers. After a few years of this sort of use, designers such as Robert J. Lang, Meguro Toshiyuki, Jun Maekawa and Peter Engel began to design using crease patterns. This allowed them to create with increasing levels of complexity, allowing the art of origami to reach unprecedented levels of realism. Now most higher-level models are accompanied by crease patterns.
Robert J. Lang, An Origami Maverick
Robert J. Lang, an origami maverick whose work has appeared at the Museum of Modern Art in New York, says his designs are inspired by the natural world. He also believes many people have a misconception about math. Lang quit his job as an engineer in 2001 to focus solely on origami — a discipline that is no less complicated. '[Math] is much broader than you may think,' he says. 'It's the study of shapes and relationships and forms.'

- www.wired.com/culture/art/magazine/16-07/mf_origami
- www.langorigami.com/art/creasepatterns/creasepatterns.php4
Mathematics of Paper Folding
The art of paper folding, or origami, has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability (whether the model can be flattened without damaging it) and the use of paper folds to solve mathematical equations.
Pure Origami
Some classical construction problems of geometry — namely trisecting an arbitrary angle, or doubling the volume of an arbitrary cube — are proven to be unsolvable using compass and straightedge, but can be solved using only a few paper folds. Paper folds can be constructed to solve equations up to degree 4. (The Huzita–Hatori axioms are one important contribution to this field of study.) Complete methods for solving all equations up to degree 4 by applying such methods are discussed in detail in Geometric Origami.
As a result of origami study through the application of geometric principles, methods such as Haga's theorem have allowed paperfolders to accurately fold the side of a square into thirds, fifths, sevenths, and ninths. Other theorems and methods have allowed paperfolders to get other shapes from a square, such as equilateral triangles, pentagons, hexagons, and special rectangles such as the golden rectangle and the silver rectangle. Methods for folding all regular polygons up to and including the regular 19-gon have been developed.
Assigning a crease pattern mountain and valley folds in order to produce a flat model has been proven by Marshall Bern and Barry Hayes to be NP complete. Further references and technical results are discussed in Part II of Geometric Folding Algorithms.
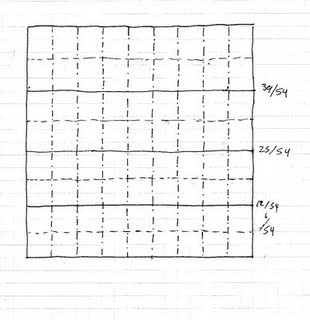
Kawasaki's theorem states that a given crease pattern can be folded to produce a flat model if and only if all the sequences of angles a1,...,a2n surrounding each vertex fulfill the condition that a1 + a3 + ... + a2n-1 = a2 + a4 + ... + a2n = 180°; in other words, the sum of every other angle surrounding an interior vertex is always equal to 180°.
- en.wikipedia.org/wiki/Mathematics_of_paper_folding
- origamido-en.blogspot.com/2008/05/months-ago-when-i-get-envolved-with.html
Origami Furniture
Foldschool is a collection of free cardboard furniture for kids, handmade by you. The downloadable patterns can be printed out with any printer. Follow the instructions and assemble a stable piece of furniture.

- first mode:studying, reading, writing,
- second mode: comfortable sitting for relaxation and contemplation
- third mode: informal conferencing
- transformers you can use in two (or more) different ways without changing mode
- transformers that change modes (the chair turns into...)
- accessories are attached to the chair (linked)
- accessories in use only for one mode, can be taken apart